Aljabar Boolean
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Dalam matematika dan ilmu komputer, Aljabar Boolean adalah struktur aljabar yang "mencakup intisari" operasi logika AND, OR dan NOR dan juga teori himpunan untuk operasi union, interseksi dan komplemen.Penamaan Aljabar Boolean sendiri berasal dari nama seorang matematikawan asal Inggris, bernama George Boole. Dialah yang pertama kali mendefinisikan istilah itu sebagai bagian dari sistem logika pada pertengahan abad ke-19.
Boolean adalah suatu tipe data yang hanya mempunyai dua nilai. Yaitu true atau false (benar atau salah).
Pada beberapa bahasa pemograman nilai true bisa digantikan 1 dan nilai false digantikan 0.
Daftar isi[sembunyikan] |
bool my_variable = true;
if (my_variable) {
printf("True!\1");
} else {
printf("False!\0");
}
Javascript
Pengecekan tipe data boolean pada javascriptvar myVar = new Boolean(true);
if ( myVar ) {
alert("boolean");
} else {
alert("bukan boolean");
}
PHP
PHP memiliki tipe data boolean dengan dua nilai true dan false (huruf besar atau kecil tidak berpengaruh).<?php
$myVar = true;
$myString = 'String';
if (is_bool ($myVar)) {
echo "boolean";
} else {
echo "bukan boolean";
}
if (is_bool ($myString)) {
echo "boolean"
} else {
echo "bukan boolean";
}
?>
Nilai yang ekuivalen dengan false adalah:- false
- zero
- "0"
- NULL
- array kosong
- string kosong
Karnaugh mapFrom Wikipedia, the free encyclopedia
For former radio station KMAP (1962-1968) in Dallas-Fort Worth, see KRLD-FM. The Karnaugh map (K-map for short), Maurice Karnaugh's 1953 refinement of Edward Veitch's 1952 Veitch diagram, is a method to simplify Boolean algebra expressions. The Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability, permitting the rapid identification and elimination of potential race conditions.In a Karnaugh map the boolean variables are transferred (generally from a truth table) and ordered according to the principles of Gray code in which only one variable changes in between adjacent squares. Once the table is generated and the output possibilities are transcribed, the data is arranged into the largest possible groups containing 2n cells (n=0,1,2,3...)[1] and the minterm is generated through the axiom laws of boolean algebra.
ExampleKarnaugh maps are used to facilitate the simplification of Boolean algebra functions. The following is an unsimplified Boolean Algebra function with Boolean variables A, B, C, D, and their inverses. They can be represented in two different notations:
Truth tableUsing the defined minterms, the truth table can be created:
Karnaugh mapThe input variables can be combined in 16 different ways, so the Karnaugh map has 16 positions, and therefore is arranged in a 4 × 4 grid.The binary digits in the map represent the function's output for any given combination of inputs. So 0 is written in the upper leftmost corner of the map because ƒ = 0 when A = 0, B = 0, C = 0, D = 0. Similarly we mark the bottom right corner as 1 because A = 1, B = 0, C = 1, D = 0 gives ƒ = 1. Note that the values are ordered in a Gray code, so that precisely one variable changes between any pair of adjacent cells. After the Karnaugh map has been constructed the next task is to find the minimal terms to use in the final expression. These terms are found by encircling groups of 1s in the map. The groups must be rectangular and must have an area that is a power of two (i.e. 1, 2, 4, 8…). The rectangles should be as large as possible without containing any 0s. The optimal groupings in this map are marked by the green, red and blue lines. Note that groups may overlap. In this example, the red and green groups overlap. The red group is a 2 × 2 square, the green group is a 4 × 1 rectangle, and the overlap area is indicated in brown. The grid is toroidally connected, which means that the rectangular groups can wrap around edges, so  is a valid term, although not part of the minimal set—this covers Minterms 8, 10, 12, and 14. is a valid term, although not part of the minimal set—this covers Minterms 8, 10, 12, and 14.Perhaps the hardest-to-visualize wrap-around term is  which covers the four corners—this covers minterms 0, 2, 8, 10. which covers the four corners—this covers minterms 0, 2, 8, 10.SolutionFor the Red grouping:
 For the Green grouping we see that A,B maintain the same state, but C and D changes. B is 0 and has to be negated before it can be included. Thus the second term is  In the same way, the Blue grouping gives the term  The solutions of each grouping are combined into: 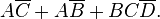 InverseThe inverse of a function is solved in the same way by grouping the 0s instead.The three terms to cover the inverse are all shown with grey boxes with different colored borders:
Don't caresThe example to the right is the same above example but with minterm 15 dropped and replaced as a don't care. This allows the red term to expand all the way down and, thus, removes the green term completely. This yields the new minimum equation:  . In this case, the don't care has dropped a term (the green); simplified another (the red); and removed the race hazard (the yellow as shown in a following section). . In this case, the don't care has dropped a term (the green); simplified another (the red); and removed the race hazard (the yellow as shown in a following section).Also, since the inverse case no longer has to cover minterm 15, minterm 7 can be covered with  rather than rather than  with similar gains. with similar gains.Race hazardsEliminationKarnaugh maps are useful for detecting and eliminating race hazards. Race hazards are very easy to spot using a Karnaugh map, because a race condition may exist when moving between any pair of adjacent, but disjointed, regions circled on the map.
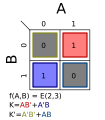
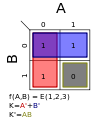
In this case, an additional term of  would eliminate the potential race hazard, bridging between the green and blue output states or blue and red output states: this is shown as the yellow region. would eliminate the potential race hazard, bridging between the green and blue output states or blue and red output states: this is shown as the yellow region.The term is redundant in terms of the static logic of the system, but such redundant, or consensus terms, are often needed to assure race-free dynamic performance. Similarly, an additional term of  must be added to the inverse to eliminate another potential race hazard. Applying De Morgan's laws creates another product of sums expression for F, but with a new factor of must be added to the inverse to eliminate another potential race hazard. Applying De Morgan's laws creates another product of sums expression for F, but with a new factor of  . .2-variable map examplesThe following are all the possible 2-variable, 2 × 2 Karnaugh maps. Listed with each is the minterms as a function of ∑() and the race hazard free (see previous section) minimum equation.See also
References
Further reading
External links
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 ).
).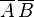


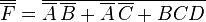

















bang tolong baigrommya jangan itu gak keliatan
BalasHapusThanks for nice information
BalasHapusdont forget to visit our site